Answer 2
a
The matrix k would encourage on the solution x to the above optimization problem that vehicles travel with constant speed at the intersection.
b
We experiment with our results on the data provided. We also vary the values of the parameter 
and 
and see the effects on the estimation. Separate the data set into two different sets. The first set is called the training set and you use it to estimate the travel times x. Then use the second set (called validation set) and compute the estimation error using the value of x that we computed on the training set.
| K1 training set 1 | K1 training set 2 | K1 training set 3 | K1 training set 4 | K2 training set 1 |
 |
 |
 |
 |
 |
Here's how we seperated data set:
| K | Training Set 1 | Training Set 2 | Training Set 3 | Training Set 4 | K2 | |
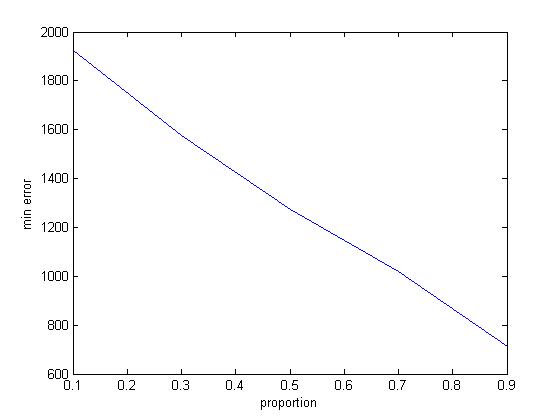
| Training Set | 1 -- 3000 | Randomly Split 50% | Random Split [0.9 0.7 0.5 0.3 0.1] | [400 1200 2000 2800 3600] | Training Set | 1 -- 3000 |
| Validation Set | 3001 -- 4419 | Randomly Split 50% | Random Split [0.1 0.3 0.5 0.7 0.9] | [3600 2800 2000 1200 400] | Validation Set | 3001 -- 4419 |
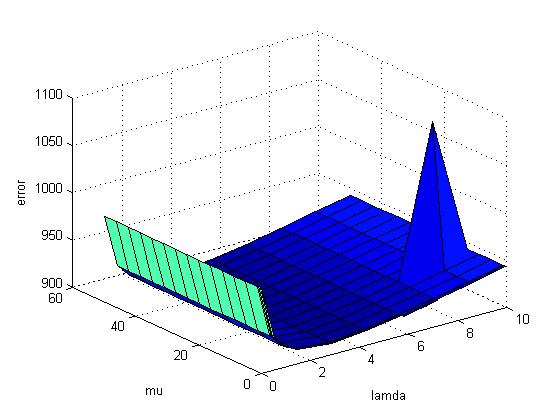
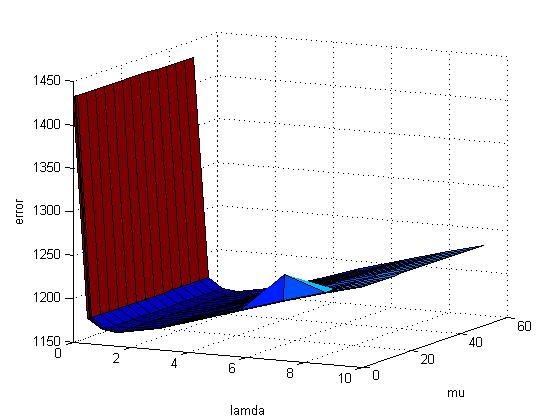
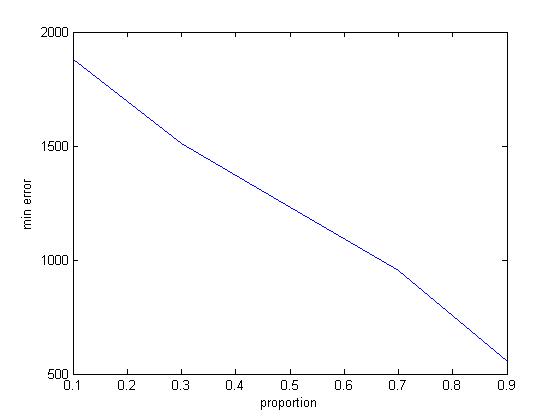
| Min error | 910.7101 | 1.16E+03 | Min error | 910.7045 | ||
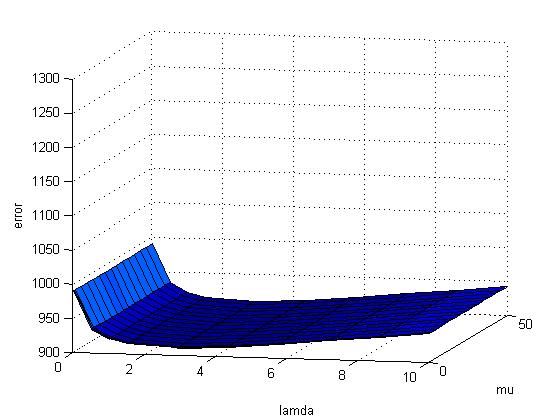
| Opt lambda | 2.9167 | 1.5 | Opt lambda | 2.9167 | ||
| Opt mu | 23.8846 | 1.5 | Opt mu | 23.8846 |
Note that the error has a positive linear relationship with lamda. The reason is in reality traffic pattern deviates from the average traffic pattern. Thus, when we try to approximate x to x_hat, the error is growing.
c
We also experimented with a similar K matrix to that described above. Instead of considering incoming/outgoing pairs, however, our second matrix considered n-1 pairwise differences between link speeds, effectively attempting to maintain the same speed for all links in an intersection using the l-1 norm trick
